Standard Deviation Calculator
Contents
- 1 Standard Deviation Calculator: Your Guide to Statistics
- 1.1 What is Standard Deviation?
- 1.2 How to Calculate Standard Deviation
- 1.3 Why Standard Deviation Matters
- 1.4 Frequently Asked Questions
- 1.4.1 What’s the difference between standard deviation and variance?
- 1.4.2 Can a standard deviation be a negative number?
- 1.4.3 How does the margin of error relate to standard deviation?
- 1.4.4 What is a “good” standard deviation?
- 1.4.5 Why do we use n-1 for a sample instead of n?
- 1.4.6 What are some other key statistical terms?
- 1.5 Conclusion
Standard Deviation Calculator
Standard Deviation Calculator: Your Guide to Statistics
Ready to demystify those intimidating statistics? Whether you’re a student tackling a homework problem or a professional analyzing data, understanding key concepts like standard deviation is crucial. This article will not only help you calculate the standard deviation for a given dataset but also explore what this powerful metric tells you about your data.
You’ve probably seen a standard deviation calculator before, but what is it actually doing? It’s providing a single number that tells you how spread out your data is. A low standard deviation means your data points are clustered tightly around the average, while a high standard deviation indicates that the data is more dispersed. In short, it’s a measure of variation. We’ll walk through how to calculate it for both a population and a sample, and we’ll even use your provided numbers—10, 12, 23, 23, 16, 23, 21, and 16—to make it easy to follow.
What is Standard Deviation?
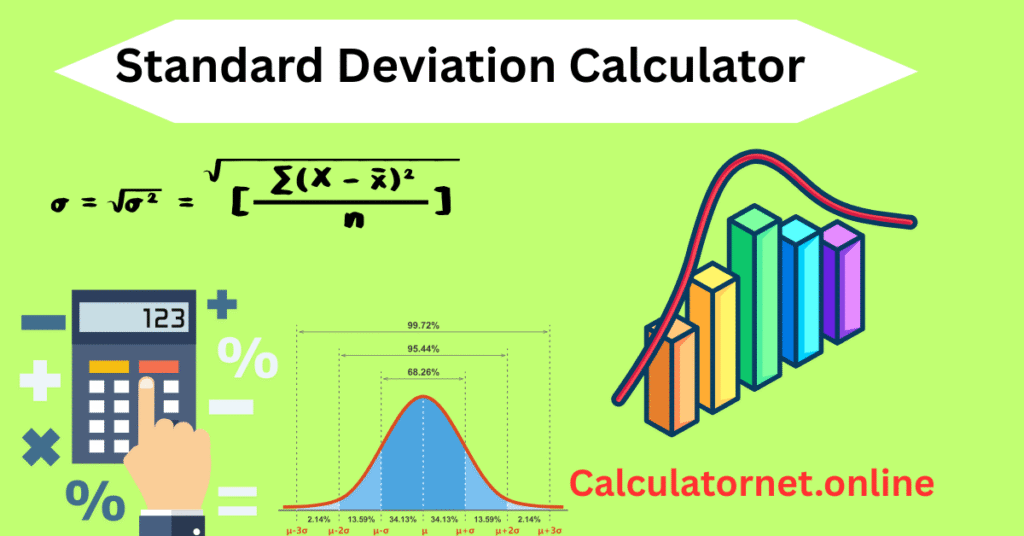
At its core, standard deviation, often represented by the symbol σ (sigma), is a measure of dispersion in a dataset. It quantifies the amount of variation or spread of a set of values. If your data points are close to the mean (the average), the standard deviation is small. If the data points are spread out over a wide range, the standard deviation is large.
Think of it like this: Imagine two cities with the same average temperature of 75°F. One city is on the coast, and its temperature rarely goes below 60°F or above 85°F. The other city is inland, and its temperature can swing from 30°F to 110°F. While their average is the same, the inland city has a much higher standard deviation because its temperatures are more spread out. This simple example shows why looking at just the average isn’t enough; you need to understand the variability, which is exactly what standard deviation provides.
How to Calculate Standard Deviation
Calculating standard deviation involves a few simple steps. The formula you use depends on whether you’re working with an entire population or just a sample of that population.
Calculating Population Standard Deviation
When you have data from an entire population, you use the population standard deviation formula:
σ=N∑(xi−μ)2
Where:
- xi is each individual value in the population.
- μ is the population mean.
- N is the total number of values in the population.
Let’s use your data: 10, 12, 23, 23, 16, 23, 21, 16.
Step 1: Find the Mean (μ)
The mean is the sum of all values divided by the number of values.
Sum = 10 + 12 + 23 + 23 + 16 + 23 + 21 + 16 = 144
Number of values (N) = 8
Mean (μ) = 144 / 8 = 18
Step 2: Subtract the Mean from Each Value and Square the Result
- (10 – 18)² = (-8)² = 64
- (12 – 18)² = (-6)² = 36
- (23 – 18)² = 5² = 25
- (23 – 18)² = 5² = 25
- (16 – 18)² = (-2)² = 4
- (23 – 18)² = 5² = 25
- (21 – 18)² = 3² = 9
- (16 – 18)² = (-2)² = 4
Step 3: Find the Average of the Squared Differences
This value is called the variance.
Sum of squared differences = 64 + 36 + 25 + 25 + 4 + 25 + 9 + 4 = 192
Variance = 192 / 8 = 24
Step 4: Take the Square Root of the Variance
Standard Deviation (σ) = 24 ≈ 4.899
Calculating Sample Standard Deviation
If your data is just a sample of a larger population, the formula changes slightly to account for the fact that a sample may not perfectly represent the whole population.
s=n−1∑(xi−xˉ)2
Where:
- xi is each individual value in the sample.
- xˉ (x-bar) is the sample mean.
- n is the total number of values in the sample.
Using the same dataset, the steps are the same, but in Step 3, you’ll divide by n-1 instead of n.
Variance = 192 / (8 – 1) = 192 / 7 ≈ 27.4286
Standard Deviation (s) = 27.4286 ≈ 5.237
Why Standard Deviation Matters
Understanding standard deviation has real-world applications in many fields.
- Finance: Investors use standard deviation to measure the volatility and risk of a stock. A stock with a high standard deviation is riskier because its price fluctuates more dramatically, while a stock with a low standard deviation is more stable.
- Quality Control: In manufacturing, companies use standard deviation to ensure a product stays within a certain range. For instance, if a beverage bottle must contain 12 ounces of liquid, a low standard deviation in the fill volume means the bottling process is precise and consistent.
- Weather and Climate: As we saw in our city example, standard deviation helps meteorologists and climate scientists understand how much temperatures vary from the average, providing a more complete picture of a region’s climate.
Frequently Asked Questions
What’s the difference between standard deviation and variance?
Variance is the average of the squared differences from the mean, while standard deviation is the square root of the variance. Standard deviation is often preferred because it’s in the same units as the original data, making it easier to interpret.
Can a standard deviation be a negative number?
No, standard deviation is always a non-negative number. Since it is the square root of the variance, and variance is a sum of squared values, it can never be negative. A standard deviation of zero means all data points are identical.
How does the margin of error relate to standard deviation?
In statistics, the standard error of the mean is a special type of standard deviation that measures the accuracy of the sample mean as an estimate of the population mean. This is what’s used to calculate the margin of error in surveys and polls.
What is a “good” standard deviation?
There is no universal “good” or “bad” standard deviation. Its value is only meaningful when you compare it to the mean or to the standard deviation of another dataset. A small standard deviation is good if you want consistency, but a large one might be good if you are looking for wide-ranging possibilities, such as in certain investment strategies.
Why do we use n-1 for a sample instead of n?
Using n-1 in the denominator for a sample calculation is known as Bessel’s correction. It helps to correct the bias in the sample variance, making it a better, more accurate estimate of the true population variance.
What are some other key statistical terms?
When using a standard deviation calculator, you’ll often encounter other terms:
- Mean: The average of the dataset.
- Median: The middle value of the dataset when it’s sorted.
- Mode: The value that appears most frequently in the dataset.
- Range: The difference between the highest and lowest values.
Conclusion
The Standard Deviation Calculator isn’t just a tool for crunching numbers; it’s a window into the spread and variability of your data. By understanding the concept of standard deviation, you gain a deeper insight into the consistency and reliability of everything from test scores to financial market trends. The next time you see this term, you’ll know exactly what it means and why it’s so important.
Have you used a standard deviation calculator for a project or class? Share your experience in the comments below!